Cryptography

。

[TOC]

Starting

grading policy

50 期末考

50 平时作业（查重）

更详细的讲义走这里：http://cc.zju.edu.cn/bhh/crypto.doc

一些解密：zju_school_bus

主要内容

。编程工具：http://cc.zju.edu.cn/bhh/VC6_Aegisys.exe

。大数库：http://cc.zju.edu.cn/bhh/openssl.rar

。官网：www.openssl.org

数学基础、古典密码、MD5、SHA-1、RC4、DES、AES、RSA、ECC

DES和AES是对称密码学算法（加密解密同一把钥匙），RSA和ECC是非对称的

数学基础

整除

$b = a * k，a \mid b$

素数prime 互素relatively prime

gcd(a,b) = 1：a、b 互素，e.g. 4和9

最大公约数 greatest common divisor

a、b为整数，且至少有一个不为零，d = gcd(a,b)，则一定存在整数x、y使 a * x + b * y = d

模mod 同余congruent

$a=b+n*k\;(k\in Z),\;a\equiv b\mod n$

逆元inverse

a是b的加法模n逆元：$a+b\equiv 0 \mod n$

a是b的乘法模n逆元：$a*b\equiv 1\mod n$，将$b$记作$a^{-1}$

利用扩展欧几里得法求乘法逆元：

e.g. $13*x\equiv 1\mod 35 \Leftrightarrow gcd(13,35)=1\Rightarrow \dots\Rightarrow x=27$

古典密码

单表密码

只使用一张密码字母表，且明文字母与密文字母有固定对应关系。频率分析法可以对付单表密码

Edgar Allan Poe “The Gold-Bug”, Arthur Conan Doyle“The Dancing Men”

加法密码-凯撒密码

e.g. $y=(x+3)\% 26,\;x=(y+23)\%26$

乘法密码

加密算法：$y=x*k\%n$

解密算法：$x=y*k^{-1}\%n$

仿射密码

加密算法：$y=(x*k1+k2)\%n$

解密算法：$x=(y-k2)*k_1^{-1}\%n$

多表密码

明文与密文字母没有固定对应关系（同一明文字母对应密文会变）

Enigma ：http://cc.zju.edu.cn/bhh/enigma.rar

先转动齿轮，再对键盘输入信号进行修改；
接线板只影响键盘输入和灯泡输出；
密文字母一定不等于明文字母（reflector对应必不相同）；
明文 -> plugboard -> rotor (3) -> reflector -> rotor(3)（反查表） ->plugboard -> 暗文

注意按逆向路径经过3个齿轮时要反查表；
Ring Setting是齿轮内部的初始状态，它们在齿轮转动时不会发生变化。

而齿轮外部的状态MessageKey是会随每一次按键而发生变化的。

Δ = MessageKey - RingSetting，进入每一个齿轮时，需要先加上Δ，出去时要减掉
5个齿轮使下一个齿轮发生跳转的字母:

QEVJZ：齿轮的当前位置，从左到右对应齿轮I II III IV V

RFWKA：齿轮的下一步位置

齿轮	ABCDEFGHIJKLMNOPQRSTUVWXYZ
I	EKMFLGDQVZNTOWYHXUSPAIBRCJ
II	AJDKSIRUXBLHWTMCQGZNPYFVOE
III	BDFHJLCPRTXVZNYEIWGAKMUSQO
IV	ESOVPZJAYQUIRHXLNFTGKDCMWB
V	VZBRGITYUPSDNHLXAWMJQOFECK

double stepping:

由Enigma的机械结构决定的，该现象只会出现在中间那个齿轮上

II当前在E位置, I不管在什么位置，旋转I都会带动II转（假设使用III,II,I）
密码本给出日期、选择的齿轮和顺序、Ring setting、接线板连接字母对、一串和日期有关的代码
MessegeKey传递：先通过无线电传明文（假设为ABC），收报方暂时将MessageKey设为该值（ABC）；再把当天MessageKey（假设为XYZ）加密（X’Y‘Z’）发给对方，对方解密出MessageKey后开始通讯

图灵采用了“已知明文攻击”的方法破解Enigma

hash函数

MD5

$plaintext\;明文\leftrightarrow ciphertext\;密文$

$message\;报文\rightarrow digest\;摘要$

md5算法算出的结果是32位以16进制表示的数（128位，即16字节）（报文可以无限长，也可以为空）

只能根据报文算出摘要，不能根据摘要算出报文（不属于加密解密，是单向的）

相当于有损压缩（压缩过程中特意丢弃一些信息），可以用来验证下载的文件是否和原始文件是同一份文件（不是严格一对一的，同一个摘要对应的报文可能有多个，但是碰撞的概率非常非常小），也可以保存用户密码到数据库（不存password而是存经md5计算后的代码）

碰撞的放大效果：m1(128字节)和m2(128字节)碰撞，则1.exe = 0.exe + m1和2.exe = 0.exe + m2也会碰撞。（文件上传网站时会经过病毒检测，如果发生碰撞则认为是同一份文件，不再进行扫描–>可以通过碰撞放大恶意传病毒文件）

切块计算：每次处理64字节的信息（明文）data[64]，计算结果保存在state[4]（即128位摘要）中，count[2]表示原始明文总长度（单位bit，1G内容是1G*8，count[0] += buf_len<<3）
种子值：state[0] = 0x67452301, state[1] = 0xEFCDAB89, state[2] = 0x98BADCFE, state[3] = 0x10325476（自己想复现上述1.exe与2.exe的碰撞，则这里的种子值应当修改为0.exe的md5结果，且只能做update不能做final）
（最后一个块）count内8字节的信息需要作为填充以小端的形式补到data末尾8字节，前面多余的部分需要填充（前面先跟一个0x80，然后用0x00填充直到剩下给count的8字节）（特殊情况：如果缓冲区buf是空的，即buf长度为0，data里没有数据，先填充0x80，再55个0x00，最后8字节的count值，事实上，buf空的count也就是0）
一般最后只需要做一次灌输，但如果最后一次buf读入超过55字节（不够填充0x80的1字节和count的8字节），则需要两次灌输：（以data[0]到data[55]已赋值为例）第一次灌输data[0]~data[55]，data[56] = 0x80，后面7字节0x00；第二次56字节0x00和8字节count（相当于填充两个块）

破解方法：rainbow table（我的评价是：世界的尽头是‘穷举’）

SHA

sha-1散列算法计算出来的hash值达160位（20 Byte），比md5多了32位

也是分块计算（64字节，最后一块不足时按照md5的方式进行填充）

数据块最后要补上表示报文总共位数的8字节

分组密码工作模式与流密码

分组密码工作模式

电子密码簿ECB

加密：$C_j=E_k(P_j)$

解密：$P_j=D_k(C_j)$

electronic codebook：方便（加密解密过程可以并行处理）；但是安全性不是很好（对于相同内容的明文段，加密后得到的密文块相同）

密文块链接模式CBC

C1 = e(P1, key, iv); C2 = e(P2, key, iv’); P1 = P2，但是C1 != C2

// initialization vector是一个随机产生的数，长度与P相同，iv’=C1 //

加密：$C_j=E_k(P_j\oplus C_{j-1} )$

解密：$P_j=D_k(C_j)\oplus C_{j-1}$

cipher block chaining：当前块的密文与前一块的密文有关；加密过程只能串行处理；解密过程可以并行处理

密文反馈模式CFB

$C’=E(iv,key),\;C[0]=C’[0] \wedge P[0]$

$new.iv={iv[1],iv[2],\dots,iv[15],C[0]}$

$new.C’=E(new.iv,key),\;C[1]=new.C’[0]\wedge P[1]$

cipher feedback：安全性高，但是效率不高（每次加密一字节，无法并行加密），可以从密文传输的错误中恢复（造成的错误有限）

流密码算法RC4

适合网络信息的实时加密和解密（逐字节解密）

根据seed_key生成真正要用的key (prepare_key)
输入和输出是同一个buf（同一个算法，输出结果写回buf）

DES算法和AES算法

Data Encryption Standard

明文64bit = 8byte；密钥64bit = 8byte (实际只有56bit)；加密与解密的密钥相同

缺点：密钥太短，差分分析可以攻击des算法，sbox没有公开可能有后门

des框架：

// L[0]表示明文左32位, R[0]表示明文右32位
// DES加密需要做16轮循环, 循环轮号以1为基数
// K[0]表示DES的初始64位密钥
// K[i]表示第i轮加密时用到的56位密钥
des_encrypt()
{
	for(i=1; i<=16; i++)
	{
		if(i%2==1) // 奇数轮加密L[i]
		{
			L[i] = L[i-1] ^ f(K[i], R[i-1]);
			R[i] = R[i-1];
		}
		else // 偶数轮加密R[i]
		{
			R[i] = R[i-1] ^ f(K[i], L[i-1]);
			L[i] = L[i-1];
		}
	}
	t = L[16];
	L[16] = R[16];
	R[16] = t;
}

des_decrypt()
{
	for(i=16; i>=1; i--)
	{
		if(i%2==0) // 偶数轮解密L[i]
		{
			L[i-1] = L[i] ^ f(K[i], R[i]);
			R[i-1] = R[i];
		}
		else // 奇数轮解密R[i]
		{
			R[i-1] = R[i] ^ f(K[i], L[i]);
			L[i-1] = L[i];
		}
	}
	t = L[i];
	L[i] = R[i];
	R[i] = t;
}

long f(K[i], D[i])
{
   K48 = Shrink(K[i]);
	D48 = Expand(D[i]);
	return query_sbox(K48 ^ D48);   
}

(1) 64位明文在进入加密前有一个打乱的过程，此时要用到一张打乱表(static char ip[64])，把64位的顺序打乱,例如: ip[0]=58表示源数据中的第58位(实际是第58-1=57位，base 0)要转化成目标数据中的第0位，其中下标代表的是以0为基数的目标位，而数组的元素值代表的是以1为基数的源位;（下标是0到63变化，值是1到64）
(2) 64位明文经过加密变成密文后还要有一个打乱的过程，此时要用到的打乱表为static char fp[64]; fp[57] = 1表示源第0位变成目标第57位
(3) 8个sbox转化出来32位结果也需要打乱, 这张打乱表为 static char sbox_perm_table[32];
(4) 64位密钥要砍掉8位变成56位, 此时要用到一张表: static char key_perm_table[56];
(5) 56位密钥在循环左移后,要提取其中的48位,此时也要用到一张表: static char key_56bit_to_48bit_table[48];

56位变48位：100011–>a[3][1]:

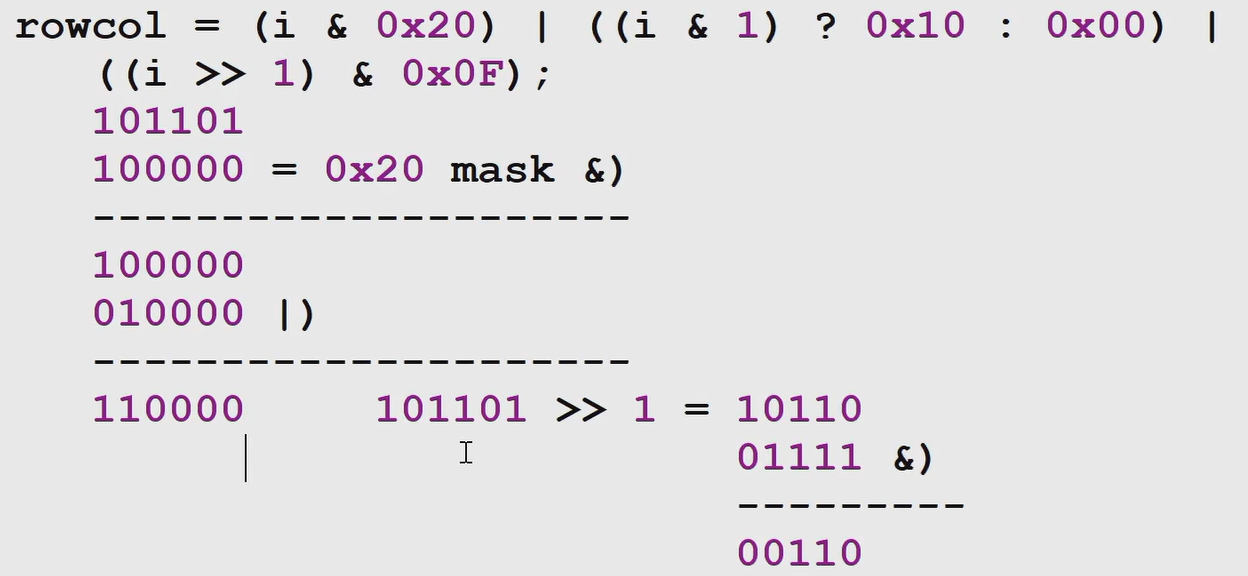
des算法中位的编号采用大端（从右到左编号，基数为1）：

b[0]		b[1]		b[2]
1011 0110	0101 1111
// 第1位 第2位 ... 第64位

用查表代替打乱（下图），可以提高计算效率，是对代码的优化

智云4-8号38分小结des算法

差分分析：已知明文攻击（明文和暗文均已知，求密钥）

利用差分分析来破解des可以大大减少穷举次数（讲起来较为复杂，做了一点精简：明文原来是左右各32位，精简后为左右各6位，密钥原56后9，原sbox进6出4现在进4出3）

首先是6位扩充成8位（012345->01323245）
密钥Kn是对上一轮密钥循环左移，取高8位
把扩充而成的8位和左移后的密钥做异或xor，然后查sbox
出来6位成为密钥和另一边做异或，如此循环

上述过程可以表示为：

L1 = L0 ^ f(R0, K1);
R1 = R0;

R2 = R1 ^ f(L1, K2);
L2 = L1;

L3 = L2 ^ f(R2, K3);
R3 = R2;

整理得到 L3 = L0 ^ f(R0, K1) ^ f(R3, K3); （L0和R0是明文，L3和R3是暗文，二者均已知；但是两个未知数K1和K3不好求，因此考虑消掉一个）

E(R3^R3*)是已知的，根据它去找符合要求的E(R3)^K3 和E(R3*)^K3组合，进入sbox后的结果与L3'^L0'进行比较

二重DES算法：$c=E(E(p,K1),K2)$

有缺陷，即穷举次数并不是$2^{56*2}$次，可以用meet in the middle attack（中间人攻击）

$c1=E(p,K1)$穷举K1共$2^{56}$次得到$2^{56}$个c1，对c用K2穷举解密得$2^{56}$个p1，比对

三重DES算法：

$c=E(D(E(p,K1),K2),K3)$

$p=D(E(D(c,K3),K2),K1)$

Advanced Encryption Standard

AES前身是Rijndael（明文长度可变）

AES的明文=128位（16字节），密文=16字节

密钥长度分成三种: 128位(16字节), 192位(24字节), 256位(32字节)，对应aes循环轮数key_rounds分别是10、12、14

aes没有像des可以用差分分析这样明显的弱点，基本只能用穷举破解

基本框架：

// 以16字节密钥为例
unsigned char p[16];
unsigned char m[4][4];
unsigned char a[4] = {0x03, 0x01, 0x01, 0x02};
// 通过aes_set_key()函数把原始的k变成16*11字节
AddRoundKey(p, k); 
// 调用该函数消耗k的16字节，因此进入之前k必须是(key_rounds+1)*16字节
for(i=1; i<=10; i++)
{
   ByteSub(p, 16); /* for(j=0;j<16;j++)
                p[j] = sbox[p[j]]; */
   // 提取p中各个元素，按纵向顺序填入数组m中:
    m[0][0]=p[0], m[1][0]=p[1],
    m[2][0]=p[2], m[3][0]=p[3],
	...
	m[0][3]=p[12],m[1][3]=p[13],
	m[2][3]=p[14],m[3][3]=p[15];
   ShiftRow(m);
   if(i != 10)
      MixColumn(m, a, 1); /* do mul */
   else
      MixColumn(m, a, 0); /* don't mul */
   memcpy(p, m, 16);
   AddRoundKey(p, k+i*(4*4));
}

$3x^3+x^2+x+2$在aes中是固定的（这是一个不可约多项式，可以看成一个素数，为的是能求它的乘法逆元。如果$x^4+1$位置的是一个不可约多项式，则前面这里可以随便选择）

注意这里的乘法需要mod 0x11B（一个不可约多项式，$x^8+x^4+x^3+x+1$），加法对每位mod 2（位内加法不产生进位，相当于异或）

（注意这里3*3要用二进制列竖式计算，且不产生进位。）

编程中不好操作这些算法，采用农夫算法：

首先假设结果p为0。乘数最低位是1时，把被乘数加到p上（有限域内加法，相当于异或），然后被乘数左移一位，乘数右移一位；乘数最低位是0时，只进行移位操作。若被乘数移位导致超过8位，对它mod 0x11B求模（两个数相近，除法转化成减法，有限域内相当于异或）。

unsigned int aes_8bit_mul_mod_0x101(unsigned int x, unsigned int y)
{
   /* 利用农夫算法求 x * y mod (X^8 + 1); */
   /*      8         0
          X         X
      n = 1 0000 0001 = 0x101
    */
   unsigned int p = 0; /* the product of the multiplication */
   int i;
   for (i=0; i < 8; i++)
   {
      if (y & 1) /* if y is odd, then add the corresponding y to p */
         p ^= x; /* since we're in GF(2^m), addition is an XOR */
      y >>= 1;   /* equivalent to y/2 */
      x <<= 1;   /* equivalent to x*2 */
      if (x & 0x100) /* GF modulo: if x >= 256, then apply modular reduction */
         x ^= 0x101; /* XOR with the primitive polynomial x^8 + 1 */
                     /* Actually, it's is the same as ROL. Commented by Black White. */
   }
   return p;
}

MixColumn对明文的每一列做矩阵乘法运算后，需要把乘积转化为行：

4 8 C		02 07 00 05
5 9 D	=> 	06 03 03 01
6 A E		...
7 B F		...

RSA

DES及AES属于对称密码体制(symmetric cryptosystem)，加密解密使用同一密钥

RSA算法属于公钥密码体制(public-key cryptosystem)，也称非对称密码体制(asymmetric cryptosystem)，加密密钥与解密密钥是不同的，加密密钥简称公钥(public key)，解密密钥简称私钥(private key)。

具体流程

明文的公钥加密、明文的私钥加密、密文的公钥解密、密文的私钥解密都能用同一个函数实现

RSA的数学基础

Euler函数 $\Phi(n):\text {小于n且与n互素的整数个数，例如}\Phi(5)=4$

Euler定理 $\gcd (x,n)=1 \rightarrow x^{\Phi(n)}=1\mod n$

Fermat小定理 $\text{设p为素数，且}\gcd(x,p)=1\text{，则}x^{p-1}=1\mod p\\ \text{因为p为素数时，}\Phi(p)=p-1$

Chinese Remainder Theorem 中国余数定理 $\text{设}m_1,m_2,\dots,m_r\text{两两互素，则以下同余方程组}\\ x\equiv a_i\mod m_i\;,\;i=1,2,\dots,r\\ 模M=m_1m_2m_3\dots m_r\text{的唯一解为}\\ x=\sum_{i=1}^r a_i*M_i*(M_i^{-1}\mod m_i)\mod M\text{，其中}i=1$

回顾乘法逆元: $13*x\equiv 1\mod 35 \Leftrightarrow gcd(13,35)=1\Rightarrow \dots\Rightarrow x=27$

Euler函数的乘法性质 $\text{若}n_1,n_2\text{互素，则}\Phi(n_1*n_2)=\Phi(n_1)*\Phi(n_2)$

Euler函数的乘积公式 $\Phi(n)=n*\Pi_{p\mid n}(1-1/p)\\ e.g.\;\Phi(10)=10*(1-1/2)*(1-1/5)$

算法证明

m、c、n、e、d均按大端格式保存
m的二进制位数需和n一致，例如加密m为16字节字符串“0123456789ABCDEF”，n的位数是128位
m < n

代码实现

源代码中pras->flags |= RSA_FLAG_NO_BLINDING;是为了避免加密模式下也用到密钥d（防旁路攻击的），即此时代码中加密只用到e和n

rsa生成注册码的好处：破解者无法在不修改软件exe的情况下算出正确注册码

软件打开时显示一个机器码，其中机器码m’=rsa(mac, 公钥)

软件作者: mac=rsa(m’, 私钥)，注册码sn=(mac, 私钥)

软件验证注册码: rsa(sn, 公钥)==mac

暴力破解排暗桩，修改程序逻辑（暗桩多时，可能没有排完）

公钥替换法破解（替换e和n，自己的d就可用了）（但是升级优化后会失效）

软件作者可以用vmprotect对exe加壳保护防止程序被修改

随机生成p和q：time()是1970.1.1零点到现在时间的总秒数，常被用来当成生成随机数的种子数；加入用户移动鼠标的实时坐标；截取用户桌面图片计算md5…

PKCS1_PADDING:

保证m < n (首字节填充零)
加入一些随机数来确保两次加密相同明文得到的密文不同,防止可能的攻击

例如：加密明文“ABCDE”，假定N是128位即16字节。填充后的明文为[ 00，02，8个字节非零随机数，00，“ABCDE” ] （随即填充的个数大于等于8）

数字签名

防止第三方假冒，防止发送方抵赖

A发送一封信L给B：

A加密：L’=RSA( L，B的公钥 )

A签名：M‘=RSA( MD5(L)，A的私钥 )

B解密：L=RSA( L’，B的私钥 )

B验证：M=RSA( M’，A的公钥 ) $\underset = ?$ MD5(L)

ECC

Elliptic Curve 椭圆曲线算法

Cryptography

Cryptography

。

Starting

grading policy

主要内容

数学基础

整除

素数prime 互素relatively prime

最大公约数 greatest common divisor

模mod 同余congruent

逆元inverse

古典密码

单表密码

加法密码-凯撒密码

乘法密码

仿射密码

多表密码

hash函数

MD5

SHA

分组密码工作模式与流密码

分组密码工作模式

电子密码簿ECB

密文块链接模式CBC

密文反馈模式CFB

流密码算法RC4

DES算法和AES算法

Data Encryption Standard

Advanced Encryption Standard

RSA

具体流程

RSA的数学基础

算法证明

代码实现

数字签名

ECC

results matching ""

No results matching ""